Arytmetyka modularna jest kolejnym narzędziem matematycznym ułatwiającym infomatykom rozwiązywanie problemów algorytmicznych.
Rozważmy następujące zadania:
Problem 1. Czy 13 dzieli 16971461287794?
Problem 2. Jasio kupił w sklepie dużą paczkę cukierków. Teraz zastanawia się kogo zaprosić na swoje urodziny. Jeśli zaproszę tylko Tomka i Bartka to po podzieleniu cukierków na nas troje pozostanie jeden cukierek. Jeśli przyjdzie jeszcze Kasia, to zostaną dwa cukierki. O! Ale jeśli zaproszę jeszcze Marcina, to cukierki będzie można równo podzilić. Ile cukierków było w paczce Jasia?
Problem 3. Jakie są trzy ostatnie cyfry liczby 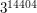 ?
?
Powyższe problemy mogą wydawać się trudne, ale wkrótce je rozwiążemy używając jedynie ołówka, kartki i... arytmetyki modularnej.
Definicja i podstawowe własności
Niech 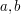 będą liczbami całkowitymi, a
będą liczbami całkowitymi, a  liczbą całkowitą dodatnią. Definiujemy kongruencje w następujący sposób:
liczbą całkowitą dodatnią. Definiujemy kongruencje w następujący sposób:
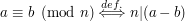
Czytamy a przystaje do b modulo n, albo a kongruentne z b.
Ciekawa i ważna własność kongruencji to taka, że 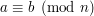 wtedy i tylko wtedy, gdy liczby
wtedy i tylko wtedy, gdy liczby  oraz
oraz 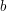 przy dzieleniu przez
przy dzieleniu przez  daje tą samą resztę. Na przykład
daje tą samą resztę. Na przykład 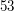 oraz
oraz 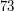 dają tą samą resztę (mianowicie
dają tą samą resztę (mianowicie 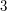 ) przy dzieleniu przez
) przy dzieleniu przez 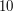 . Faktycznie zachodzi
. Faktycznie zachodzi 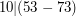 bo
bo 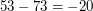 a
a 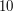 dzieli
dzieli 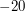 . Zatem zachodzi
. Zatem zachodzi 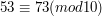 . Kolejne ważne własności kongruencji to:
. Kolejne ważne własności kongruencji to:
- Zwrotność kongruencji
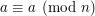
- Symetryczność kongruencji
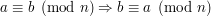
- Przechodność kongrunecji
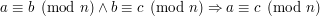
Ponadto jeśli: 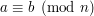 oraz
oraz 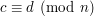 to zachodzi:
to zachodzi:
Spróbujmy udowodnić jedną z tych własności. Na przykład dodawanie i mnożenie. Resztę pozostawiam czytelnikowi do samodzielnego udowodnienia. Jeśli a jest kongruentne z b to istnieje taka liczba k, że 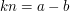 analogicznie istnieje takie l, że
analogicznie istnieje takie l, że 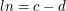 . Dodając oba równania do siebie stronami otrzymujemy, że
. Dodając oba równania do siebie stronami otrzymujemy, że 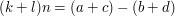 . Zatem
. Zatem 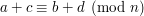 . Teraz mnożenie. Mam podobnie jak ostatnio:
. Teraz mnożenie. Mam podobnie jak ostatnio: 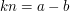 oraz
oraz 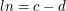 przerzućmy b oraz d na drugą stronę. Otrzymamy:
przerzućmy b oraz d na drugą stronę. Otrzymamy: 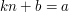 oraz
oraz 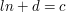 . Mnożąc stronami obie równości otrzymamy:
. Mnożąc stronami obie równości otrzymamy: 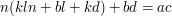 . Przerzucając
. Przerzucając 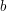 na drugą stronę otrzymamy żądaną równość.
na drugą stronę otrzymamy żądaną równość.
Z powyższych równań oraz ze zwrotności kongruencji wynika, że do obu stron kongruencji możemy dodać, odjąć jakąś liczbę całkowitą, lub pomnożyć obie strony przez dowolną liczbę całkowitą. Okazuje się, że nie zawsze można dzielić obustronnie przez dowolną liczbę. Weźmy na przykład równanie:
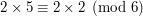
Faktycznie 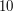 przystaje do
przystaje do  modulo
modulo 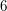 , bo
, bo 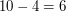 . Gdy jednak podzielimy obustronnie przez
. Gdy jednak podzielimy obustronnie przez 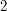 otrzymamy:
otrzymamy:
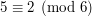
Co już nie jest prawdą, bo 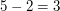 , a
, a 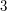 nie dzieli się przez
nie dzieli się przez 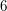 . Okazuję się, że równanie
. Okazuję się, że równanie 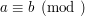 możemy obustronnie bezpiecznie podzielić przez
możemy obustronnie bezpiecznie podzielić przez 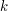 wtedy gdy liczba
wtedy gdy liczba 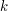 jest względnie pierwsza z
jest względnie pierwsza z  . Czyli gdy
. Czyli gdy 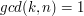 . O tym dlaczego tak jest dowiemy się w następnym rozdziale. A teraz dowiemy się jeszcze, że możemy dowolnie dzielić wszystkie trzy liczby w kongruencji:
. O tym dlaczego tak jest dowiemy się w następnym rozdziale. A teraz dowiemy się jeszcze, że możemy dowolnie dzielić wszystkie trzy liczby w kongruencji:
Jeśli 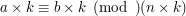 to
to 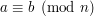 .
.
Z faktu, że możemy dodawać, odejmować i mnożyć wynika następujący wniosek: Jeśli 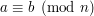 to dla dowolnego wielomianu
to dla dowolnego wielomianu 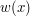 o współczynnikach całkowitych:
o współczynnikach całkowitych: 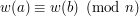 .
.
Dla przykładu niech 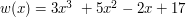 . Skoro wiemy, że
. Skoro wiemy, że 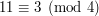 to musi zachodzić
to musi zachodzić 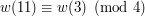 . Faktycznie! Przecież:
. Faktycznie! Przecież:
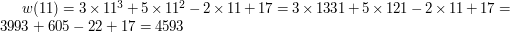
natomiast 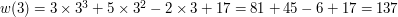 , a
, a 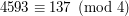 bo
bo 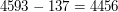 , a przecież
, a przecież  dzieli
dzieli 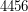 bo
bo 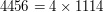 .
.




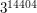 ?
?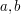 będą liczbami całkowitymi, a
będą liczbami całkowitymi, a  liczbą całkowitą dodatnią. Definiujemy kongruencje w następujący sposób:
liczbą całkowitą dodatnią. Definiujemy kongruencje w następujący sposób: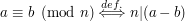
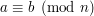 wtedy i tylko wtedy, gdy liczby
wtedy i tylko wtedy, gdy liczby  oraz
oraz 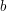 przy dzieleniu przez
przy dzieleniu przez 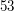 oraz
oraz 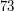 dają tą samą resztę (mianowicie
dają tą samą resztę (mianowicie 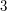 ) przy dzieleniu przez
) przy dzieleniu przez 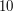 . Faktycznie zachodzi
. Faktycznie zachodzi 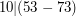 bo
bo 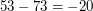 a
a 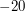 . Zatem zachodzi
. Zatem zachodzi 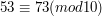 . Kolejne ważne własności kongruencji to:
. Kolejne ważne własności kongruencji to: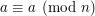
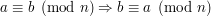
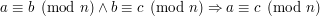
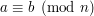 oraz
oraz 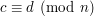 to zachodzi:
to zachodzi: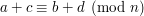
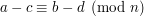
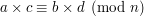
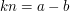 analogicznie istnieje takie l, że
analogicznie istnieje takie l, że 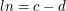 . Dodając oba równania do siebie stronami otrzymujemy, że
. Dodając oba równania do siebie stronami otrzymujemy, że 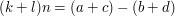 . Zatem
. Zatem 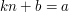 oraz
oraz 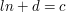 . Mnożąc stronami obie równości otrzymamy:
. Mnożąc stronami obie równości otrzymamy: 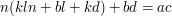 . Przerzucając
. Przerzucając 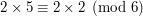
 modulo
modulo 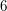 , bo
, bo 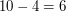 . Gdy jednak podzielimy obustronnie przez
. Gdy jednak podzielimy obustronnie przez 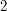 otrzymamy:
otrzymamy: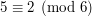
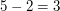 , a
, a 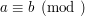 możemy obustronnie bezpiecznie podzielić przez
możemy obustronnie bezpiecznie podzielić przez 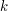 wtedy gdy liczba
wtedy gdy liczba 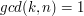 . O tym dlaczego tak jest dowiemy się w następnym rozdziale. A teraz dowiemy się jeszcze, że możemy dowolnie dzielić wszystkie trzy liczby w kongruencji:
. O tym dlaczego tak jest dowiemy się w następnym rozdziale. A teraz dowiemy się jeszcze, że możemy dowolnie dzielić wszystkie trzy liczby w kongruencji: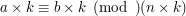 to
to 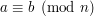 .
.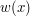 o współczynnikach całkowitych:
o współczynnikach całkowitych: 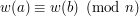 .
.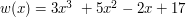 . Skoro wiemy, że
. Skoro wiemy, że 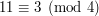 to musi zachodzić
to musi zachodzić 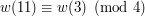 . Faktycznie! Przecież:
. Faktycznie! Przecież: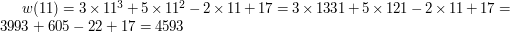
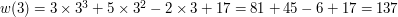 , a
, a 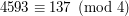 bo
bo 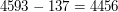 , a przecież
, a przecież 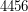 bo
bo 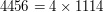 .
.

