Funkcją malowane, czyli słów kilka o fraktalach
02.12.2009 - Wiktor Zychla
  Czym są fraktaleMatematycy w swojej codziennej pracy zajmują się poznawaniem mnóstwa własności, którym nie sposób odmówić elegancji czy wręcz specyficznego piękna. Często mówi się wręcz, że matematyka jest dziedziną sztuki tak samo jak nauki.Pewien drobny niuans tak pojmowanego piękna matematyki polega na tym, że aby móc je choć trochę pojąć i docenić, trzeba mimo wszystko dysponować dość specyficznym poczuciem estetyki, które kształtuje się przez lata spędzone w świecie aksjomatów, twierdzeń, liczb, figur, reguł czy funkcji. Istnieją jednak (a może 'na szczęście'?) takie twory myśli matematycznej, których piękno dostrzeże nie tylko specjalista o wykształconej wrażliwości. Tymi tworami są obiekty fraktalne. Wbrew popularnej definicji, zgodnie z którą fraktalami są takie twory geometryczne, które charakteryzują się jakąś formą samopodobieństwa, matematycy częściej przyjmują definicję szerszą, w której samopodobieństwo jest tylko jednym z kryteriów fraktalności. Jest bardzo wiele rodzajów fraktali, tych popularnych jak trójkąt Sierpińskiego czy zbiór Mandelbrota oraz mniej znanych. W tym artykule obejrzymy trzy przykłady zbiorów o charakterze fraktalnym, oparte na zupełnie innych podstawach matematycznych, a równie fascynujące w swojej reprezentacji graficznej. Trójkąt SierpińskiegoTrójkąt Sierpińskiego jest jednym z najlepiej opisanych fraktali. Jego konstrukcja polega na "wycięciu" środka dowolnego trójkąta (rozumianego przez trójkąt wewnętrzny powstały przez połączenie środków wszystkich trzech boków), a następnie powtarzanie tego postępowania dla pozostałych trójkątów.
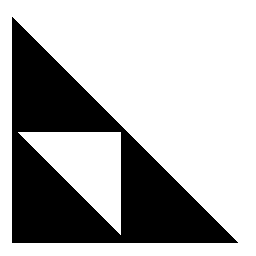
To co otrzymujemy w efekcie "nieskończonego" powtarzania tego procesu (czy w ogóle można umawiać sie, że jakieś czynności wykonujemy "w nieskończoność"?) jest właśnie trójkątem Sierpińskiego.
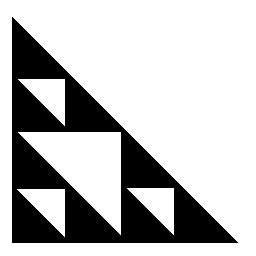
Najbardziej zaskakujące w trójkącie Sierpińskiego jest to, że pierwotny "przepis" na jego otrzymanie jest jednym z wielu zupełnie różnych przepisów, tym ciekawszych, im mniej oczywistych, a prostych w definicji i ewentualnej implementacji w postaci programu komputerowego. Do moich ulubionych przepisów "alternatywnych" należą trzy:
Ostatni z tych przepisów zaimplementowany jest w postaci przykładowej aplikacji uruchamianej w oknie przeglądarki. Aby obejrzeć działanie programu, wymagana jest przeglądarka obsługująca formant typu Canvas. Zachęca się Czytelnika do wykorzystania kodu aplikacji do zaimplementowania pozostałych algorytmów.
Trójkąt Sierpińskiego ma wiele interesujących rozwinięć, nie tylko na płaszczyźnie, ale także w przestrzeni (piramida Sierpińskiego, gąbka Mengera). Ogólna zasada, na której zbudowane są zbiory samopodobne tego typu, nazywa się IFS (ang. Iterated Function System) i polega na opisaniu przekształceń zwężających na płaszczyźnie a następnie znajdowaniu zbiorów, które są niezmienne względem takiego układu przekształceń. Najbardziej znanymi fraktali typu IFS są smok Heighwaya, paproć Barnsleya i fraktalne drzewo. . 

|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com





