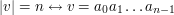Podstawy algorytmów tekstowych
25.11.2009 - Damian Rusak
 Aby przyswoić zasady działania algorytmów tekstowych trzeba znać podstawowe zagadnienia i definicje z tej dziedziny. Może się wydawać, że nie ma nic bardziej intuicyjnego od posługiwania się tekstem i językiem, jednak to co te pojęcia oznaczają z informatycznego punktu widzenia może być początkowo zaskakujące. Poniższy artykuł ma na celu prezentację (mam nadzieję, w miarę ciekawy sposób) terminologii, której znajomość pozwala nauczyć się wielu fascynujących algorytmów tekstowych. Zacznijmy może od strony "technicznej" - jak matematycznie i dokładnie sformułować to, czym chcemy się zajmować? Każdy tekst składa się z pewnych symboli - nasz korzysta z liter, cyfr, znaków przestankowych i wielu innych. Nie ma większego sensu ograniczać się w tej kwestii - przyjmijmy, że symbole mogą być dowolne. Zbiór symboli, z którego będziemy korzystać nazwiemy alfabetem - oznacza się go zwyczajowo jako
ale równie dobrze alfabetem może być zbiór
Każdy symbol jest jednakowo dobry - to tylko pewien obiekt, któremu można nadać matematyczne znaczenie. Oczywiście, skoro mamy dowolność, najwygodniej będzie korzystać z liter alfabetu angielskiego - i z taką konwencją będziemy się najczęściej spotykać w zadaniach informatycznych. Teraz jak alfabet wykorzystać? Otóż z symboli będziemy tworzyć słowa. Słowo to po prostu skończony ciąg symboli z alfabetu. Z alfabetu Czy słowo może nie składać się z żadnego symbolu? Owszem, z wielu powodów przyjmujemy, że zawsze mamy słowo puste - odpowiednik zera w liczbach naturalnych czy zbioru pustego. Słowo puste zwyczajowo oznaczamy grecką literą epsilon - Widzimy, że słów można stworzyć bardzo wiele - jest też matematyczne pojęcie na zbiór słów - to język. Oczywiście musimy porzucić intuicje z "rzeczywistego" świata - słowa nie muszą mieć żadnego sensu w języku polskim, ani w żadnym innym "ludzkim" języku. Język zatem to pewien zbiór słów, spośród wszystkich, jakie tylko możemy stworzyć. Rysunek poniżej pokazuje nam przykład alfabetu i nieskończonego języka nad nim, który zawiera wszystkie słowa możliwe do utworzenia - taki język oznaczamy jako
Właśnie - napisałem, że język jest nad alfabetem, a na rysunku znajduje się poniżej... To po prostu konwencja matematyczna - mówimy, że język jest nad alfabetem, gdy wszystkie słowa z tego języka są stworzone za pomocą symboli alfabetu. Wiemy już, jak oznaczyć język zawierający wszystkie możliwe słowa, możemy więc wprowadzić formalną definicję języka:
Innymi słowy, jeśli Możemy mówić też o języku pustym - Najwyższy czas by formalizm zaatakował też pojęcie słowa. Na oznaczenie słów najczęściej będziemy używać liter
Dla wygody i szybkiego dostępu do symboli składających się na słowo wprowadźmy sobie indeksy kolejnych "liter" słowa: jeśli Np. jeśli Zauważ, że numerujemy symbole słowa począwszy od zera - to przyjęta w informatyce konwencja indeksowania. Może się to kojarzyć np. z indeksowaniem tablic w wielu językach programowania - istotnie, często napisy są reprezentowane przez tablice znaków. Nietrudno będzie zdefiniować długość słowa - to po prostu ilość symboli, z których się składa. Oznacza się to tak, jak wartość bezwględną liczby albo długość odcinka. Będziemy pisali: Długość słowa
(10 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


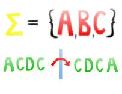
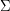 . Możemy na przykład korzystać z alfabetu:
. Możemy na przykład korzystać z alfabetu:
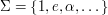 . Pełna dowolność. Albo taki alfabet jak poniżej:
. Pełna dowolność. Albo taki alfabet jak poniżej: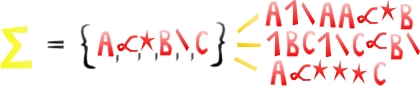
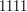 ,
, 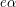 ,
, 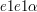 i nieskończenie wiele innych - chociażby każde słowo składające się tylko z symbolu
i nieskończenie wiele innych - chociażby każde słowo składające się tylko z symbolu 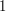 .
.  . Do czego nam to przydatne? Przekonamy się wkrótce, że dobrze mieć takie "nic" pod ręką.
. Do czego nam to przydatne? Przekonamy się wkrótce, że dobrze mieć takie "nic" pod ręką.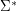 .
.
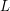 jest językiem nad alfabetem
jest językiem nad alfabetem 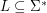 .
.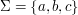 językami są na przykład
językami są na przykład 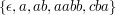 ,
, 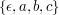 ,
, 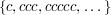 .
.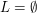 . Zauważ, że język
. Zauważ, że język 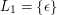 to nie to samo.
to nie to samo. 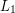 to język zawierający słowo puste, a
to język zawierający słowo puste, a 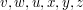 . Wiemy teraz, że:
. Wiemy teraz, że: jest słowem nad alfabetem
jest słowem nad alfabetem 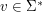 .
.
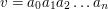 to
to 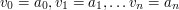 .
.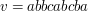 to
to 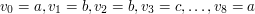 .
.