Czym jest Algorytm Euklidesa i jak taki algorytm można zapisać? Do czego służy? Jeżeli chcesz poznać odpowiedź na te pytania, zapraszamy do lektury! Ten algorytm to rzecz niezbędna dla każdego, kto chce wykorzystać w swoich programach siłę liczb.
Dwie monety - jeden problem
Nim przejdziemy do sedna sprawy, spróbujmy rozwiązać takie zadanie:
Dysponujemy monetami o dwóch nominałach - 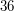 i
i 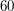 złotych (to musi być w jakiś dawnych czasach...). Chcemy za ich pomocą wypłacić tę samą kwotę - raz tylko monetami
złotych (to musi być w jakiś dawnych czasach...). Chcemy za ich pomocą wypłacić tę samą kwotę - raz tylko monetami 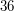 -cio złotowymi, raz tylko
-cio złotowymi, raz tylko 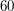 -cio złotowymi. Jaka jest najmniejsza niezerowa kwota, która spełnia te wymagania?
-cio złotowymi. Jaka jest najmniejsza niezerowa kwota, która spełnia te wymagania?
No tak, to nie jest trudne - wystarczy chwilę pomyśleć, aby znaleźć tę kwotę - to 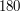 .
.
Faktycznie:
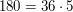
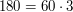
Ale dlaczego 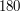 jest najmniejszą taką liczbą? Ten przykład był prosty, występowały w nim niewielkie liczby. Ale jak znaleźć odpowiedź, gdy ktoś zapyta nas o monety o nominałach
jest najmniejszą taką liczbą? Ten przykład był prosty, występowały w nim niewielkie liczby. Ale jak znaleźć odpowiedź, gdy ktoś zapyta nas o monety o nominałach 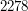 i
i 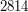 ? Albo
? Albo 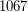 i
i 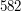 ? To wcale nietrudne!
? To wcale nietrudne!
Trochę matematyki
Na początek przypomnijmy kilka wiadomości z matematyki:
1. Mówimy, że liczba 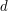 dzieli liczbę
dzieli liczbę  , jeśli istnieje taka liczba całkowita
, jeśli istnieje taka liczba całkowita 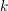 , że
, że 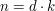 .
.
Np. 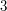 dzieli
dzieli 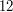 , gdyż
, gdyż 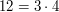 , a
, a 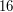 dzieli
dzieli 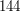 , gdyż
, gdyż 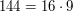 .
.
Fakt, że 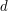 dzieli
dzieli  zapisujemy w ten sposób:
zapisujemy w ten sposób: 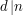 . Mamy więc
. Mamy więc 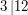 oraz
oraz 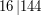 . Mówimy, że jeśli
. Mówimy, że jeśli 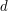 dzieli
dzieli  , to
, to 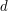 jest dzielnikiem
jest dzielnikiem  , a
, a  jest wielokrotnością
jest wielokrotnością 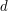 .
.
Jeżeli liczba 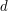 nie dzieli
nie dzieli  , będziemy pisać, że
, będziemy pisać, że 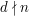 .
.
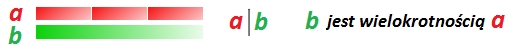
2. Jeżeli liczba 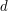 dzieli zarówno liczbę
dzieli zarówno liczbę  , jak i liczbę
, jak i liczbę 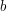 , to
, to 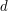 dzieli też ich różnicę,
dzieli też ich różnicę, 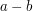 , oraz sumę
, oraz sumę 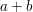 .
.
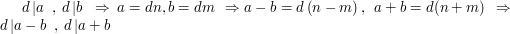
Linia powyżej mówi nam, że jeśli 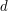 dzieli
dzieli  i dzieli
i dzieli 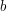 , to znaczy, że obie te liczby można zapisać jako iloczyn
, to znaczy, że obie te liczby można zapisać jako iloczyn 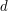 i odpowiednio
i odpowiednio  oraz
oraz 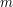 . W takim razie ich różnica,
. W takim razie ich różnica, 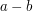 , równa jest
, równa jest 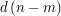 , a to oznacza, że ta różnica jest podzielna przez
, a to oznacza, że ta różnica jest podzielna przez 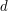 . Podobnie
. Podobnie 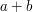 jest podzielne przez
jest podzielne przez 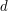 , gdyż ta suma to
, gdyż ta suma to 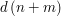 .
.

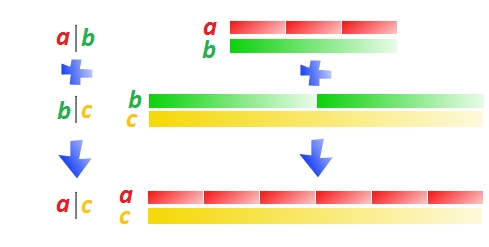
3. Jeżeli  dzieli
dzieli  , i
, i  dzieli
dzieli  , to
, to  dzieli
dzieli  .
.
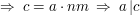
4. Jeżeli liczby  i
i 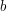 nie mają żadnego wspólnego dzielnika, większego niż jeden (czyli nie istnieje liczba większa od jeden, która dzieliłaby zarówno
nie mają żadnego wspólnego dzielnika, większego niż jeden (czyli nie istnieje liczba większa od jeden, która dzieliłaby zarówno  jaki i
jaki i 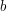 ), to mówimy, że te liczby są względnie pierwsze. Zapisujemy to w ten sposób :
), to mówimy, że te liczby są względnie pierwsze. Zapisujemy to w ten sposób : 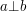 .
.
Na przykład 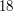 i
i 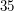 są względnie pierwsze, za to
są względnie pierwsze, za to 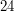 i
i 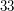 nie są względnie pierwsze, gdyż
nie są względnie pierwsze, gdyż 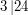 oraz
oraz 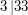 .
.
Najmniejsze i największe
Jaki mamy z tego pożytek? Powróćmy do przykładu z monetami o nominałach 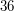 i
i 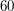 . Szukaliśmy takiej kwoty, która byłaby podzielna zarówno przez
. Szukaliśmy takiej kwoty, która byłaby podzielna zarówno przez 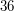 jak i przez
jak i przez 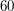 . To oznacza, że taka kwota musi się dzielić przez te same liczby, przez które dzielą się
. To oznacza, że taka kwota musi się dzielić przez te same liczby, przez które dzielą się 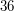 i
i 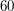 . Chcemy też, aby ta liczba była jak najmniejsza.
. Chcemy też, aby ta liczba była jak najmniejsza.
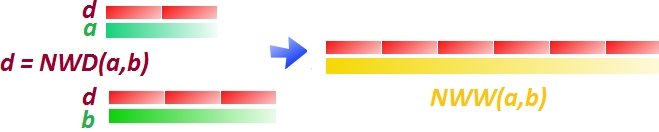
Taką najmniejszą dodatnią liczbę, podzielną przez  i przez
i przez 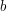 , nazywamy najmniejszą wspólną wielokrotnością i oznaczamy przez
, nazywamy najmniejszą wspólną wielokrotnością i oznaczamy przez 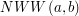 .
.
Jak ją wyznaczyć? Zauważmy, że wystarczy, aby 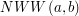 dzieliła się przez wszystkie dzielniki
dzieliła się przez wszystkie dzielniki  i
i 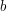 . Chcemy otrzymać liczbę jak najmniejszą, więc nie ma sensu duplikować dzielników - jeżeli jakaś liczba
. Chcemy otrzymać liczbę jak najmniejszą, więc nie ma sensu duplikować dzielników - jeżeli jakaś liczba 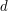 dzieli zarówno
dzieli zarówno  jak i
jak i 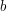 , ale
, ale 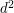 nie dzieli obu tych liczb, to nie ma sensu, aby
nie dzieli obu tych liczb, to nie ma sensu, aby 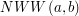 dzieliła się przez
dzieliła się przez 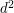 , wystarczy aby dzieliła się przez
, wystarczy aby dzieliła się przez 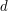 . Stąd często
. Stąd często 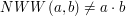 .
.
Gdybyśmy potrafili wyznaczyć największą taką liczbę, przez którą dzielą się obie liczby  i
i 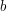 , to w łatwy sposób wyznaczylibyśmy
, to w łatwy sposób wyznaczylibyśmy 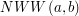 ... dlaczego?
... dlaczego?
Spójrzmy na nasz przykład - 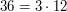 ,
, 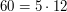 . Widzimy, że
. Widzimy, że 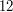 to największy wspólny dzielnik tych dwóch liczb. W takim razie ich najmniejsza wspólna wielokrotność musi być równa
to największy wspólny dzielnik tych dwóch liczb. W takim razie ich najmniejsza wspólna wielokrotność musi być równa 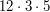 . Dlaczego? Ponieważ
. Dlaczego? Ponieważ 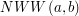 musi dzielić się przez
musi dzielić się przez 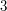 (bo
(bo 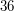 jest podzielne przez
jest podzielne przez 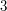 ), musi się też dzielić przez
), musi się też dzielić przez 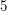 (
(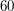 jest podzielne przez
jest podzielne przez 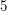 ), oraz przez
), oraz przez 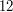 - największy wspólny dzielnik
- największy wspólny dzielnik 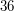 i
i 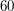 .
.
I to wszystko - każda liczba która dzieli 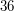 oraz dzieli
oraz dzieli 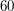 , dzieli też ich
, dzieli też ich 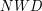 (największy wspólny dzielnik), czyli
(największy wspólny dzielnik), czyli 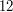 . Gdyby było inaczej, powiedzmy, że istniałaby liczba pierwsza
. Gdyby było inaczej, powiedzmy, że istniałaby liczba pierwsza 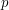 , taka, że
, taka, że 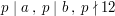 ,
, 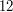 nie byłoby
nie byłoby 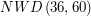 - wszak
- wszak 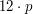 jest większe niż
jest większe niż 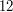 i też dzieli obie nasze liczby.
i też dzieli obie nasze liczby.
Wiemy też, że 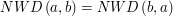 . Dlaczego?
. Dlaczego?
Wobec tego liczby 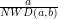 oraz
oraz 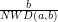 są względnie pierwsze - w
są względnie pierwsze - w 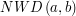 znajdują się wszystkie wspólne dzielniki
znajdują się wszystkie wspólne dzielniki  i
i 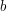 - gdy podzielimy
- gdy podzielimy  i
i 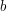 przez ich
przez ich 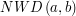 , dostaniemy liczby, które nie mogą mieć wspólnego dzielnika, większego od
, dostaniemy liczby, które nie mogą mieć wspólnego dzielnika, większego od 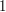 .
.
Wobec tego, wymnażając 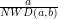 ,
, 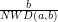
 oraz
oraz 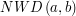 otrzymamy najmniejszą liczbę podzielną przez
otrzymamy najmniejszą liczbę podzielną przez  i przez
i przez 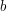 .
.
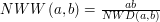
Faktycznie,  .
.




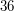 i
i 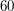 złotych (to musi być w jakiś dawnych czasach...). Chcemy za ich pomocą wypłacić tę samą kwotę - raz tylko monetami
złotych (to musi być w jakiś dawnych czasach...). Chcemy za ich pomocą wypłacić tę samą kwotę - raz tylko monetami 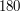 .
.
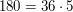
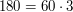
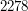 i
i 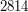 ? Albo
? Albo 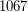 i
i 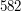 ? To wcale nietrudne!
? To wcale nietrudne!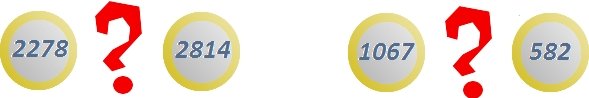
 dzieli liczbę
dzieli liczbę  , jeśli istnieje taka liczba całkowita
, jeśli istnieje taka liczba całkowita  , że
, że 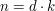 .
.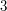 dzieli
dzieli 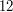 , gdyż
, gdyż 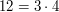 , a
, a 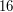 dzieli
dzieli 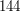 , gdyż
, gdyż 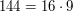 .
.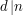 . Mamy więc
. Mamy więc 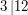 oraz
oraz 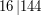 . Mówimy, że jeśli
. Mówimy, że jeśli 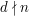 .
. , jak i liczbę
, jak i liczbę 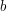 , to
, to 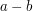 , oraz sumę
, oraz sumę 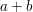 .
.
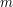 . W takim razie ich różnica,
. W takim razie ich różnica, 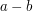 , równa jest
, równa jest 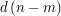 , a to oznacza, że ta różnica jest podzielna przez
, a to oznacza, że ta różnica jest podzielna przez 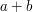 jest podzielne przez
jest podzielne przez 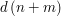 .
.
 , to
, to 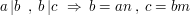
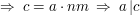
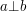 .
.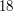 i
i 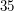 są względnie pierwsze, za to
są względnie pierwsze, za to 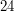 i
i 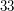 nie są względnie pierwsze, gdyż
nie są względnie pierwsze, gdyż 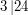 oraz
oraz 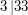 .
.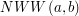 .
.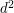 nie dzieli obu tych liczb, to nie ma sensu, aby
nie dzieli obu tych liczb, to nie ma sensu, aby 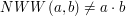 .
.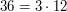 ,
, 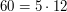 . Widzimy, że
. Widzimy, że 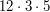 . Dlaczego? Ponieważ
. Dlaczego? Ponieważ 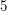 (
(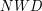 (największy wspólny dzielnik), czyli
(największy wspólny dzielnik), czyli 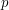 , taka, że
, taka, że 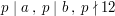 ,
, 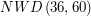 - wszak
- wszak 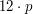 jest większe niż
jest większe niż 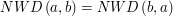 . Dlaczego?
. Dlaczego?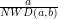 oraz
oraz 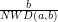 są względnie pierwsze - w
są względnie pierwsze - w 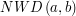 znajdują się wszystkie wspólne dzielniki
znajdują się wszystkie wspólne dzielniki 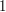 .
. oraz
oraz 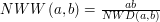
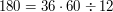 .
.


