Berek (omówienie)
14.12.2011
Zadanie było klasycznym problemem z zakresu teorii grafów. W tym wypadku rozważanym grafem jest podwórko na którym dziewczynki grały w berka - jego wierzchołkami są zakątki, a krawędziami - przejścia. W postawionym problemie wyróżniono dwa wierzchołki grafu - wierzchołek Kluczową informacją zawartą w treści zadania jest liczba krawędzi grafu - na podwórku znajduje się o jeden więcej zakątków, niż przejść; a przy tym wiadomo, że z każdego zakątka można dojść do każdego innego. Takie grafy są bardzo specyficzne - okazuje się, że graf spełniający te warunki nigdy nie zawiera cyklu, tj. z każdego zakątka do dowolnego innego prowadzi jedna i tylko jedna droga. Grafy tego rodzaju nazywamy drzewami. Wiele problemów które trudno rozwiązać dla dowolnych grafów staje się prostsze (trochę prostsze lub znacznie prostsze) kiedy ograniczymy się do drzew i tak jest w tym przypadku. Przede wszystkim zauważmy, że niezależnie od struktury podwórka i rozmieszczenia wierzchołków, Kornelia na pewno prędzej czy później złapie Joasię - dlatego, że w każdej turze będzie zwiększać się liczba wierzchołków, do których jedyna droga z aktualnego wierzchołka Joasia prowadzi przez wierzchołek Kornelii. Zastanówmy się jakie warunki musi spełniać optymalny z punktu widzenia Joasi wierzchołek końcowy (ten, w którym Kornelia łapie Joasię i gra się kończy), który oznaczymy
Tak więc dla rozwiązania tego zadania należało obliczyć odległości pomiędzy wierzchołkiem |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


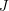 to ten, w którym znajduje się Joasia, a
to ten, w którym znajduje się Joasia, a 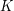 to wierzchołek w którym znajduje się Kornelia. Znając strukturę grafu należy odpowiedzieć jak długo Joasia może uciekać przed Kornelią zanim zostanie złapana, jeśli każda dziewczynka może przejść co najwyżej jedną krawędź na turę
to wierzchołek w którym znajduje się Kornelia. Znając strukturę grafu należy odpowiedzieć jak długo Joasia może uciekać przed Kornelią zanim zostanie złapana, jeśli każda dziewczynka może przejść co najwyżej jedną krawędź na turę . Przede wszystkim - odległość pomiędzy
. Przede wszystkim - odległość pomiędzy 









